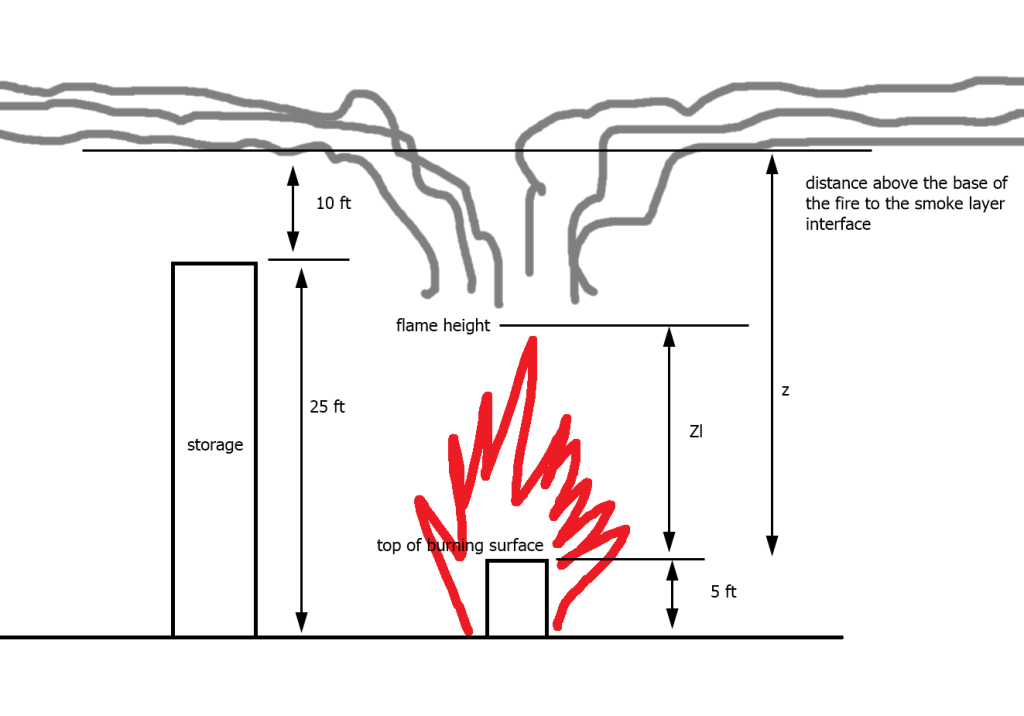
문제를 이해하려고 그림으로 그려봤다.
25ft 높이로 물건을 쌓아둔 곳에 연기층이 storage top부터 최소 10ft 이상 유지되기 위한 최소 연기 배출량은 얼마인가?
Smoke 관련이니 NFPA 92를 찾아봐야 하고, 여기서 무슨 키워드로 검색해볼까 하다가 axisymmetric으로 검색해보니 definition 건너뛰고 바로 5.5.1에 Axisymmetric plumes가 나왔다.
딱 보니 이 문제 풀기에 맞는 공식이다.
5.5.1.1을 보니 Zl이 Z보다 큰 경우와 작은 경우에 대해 공식이 나뉘어 있는데,
Z의 경우 distance above the base of the fire to the smoke layer interface라고 알아듣기 쉽게 나와 있는데 반해, zl은 limiting elevation이라고만 나와 있어서 뭔지 헷갈렸다. 연기가 깔리는 하한선인가? 싶었는데, 이 공식을 쓰는 곳이 또 있나 싶어서 0.533으로 검색해보니 Annex K에 PE문제와 완전 동일한 예제가 나왔다.
Annex K.1.2. Problem 2의 풀이과정을 보니 이해가 됐다. Zl은 flame height 였다.
PE문제에서 Zl을 계산해보면 problem 2와 동일한 열방출률 3500 BTU/s 이므로 동일한 flame height, zl, 13.9 ft가 된다.
flame height zl이 z 보다 작으므로, 5.5.1.1.b의 when z > zl 인 경우의 공식을 써서 계산해야 하고,
$$m=0.022 Q_c^{(1/3)} z^{(5/3)}+0.0042Q_c $$
에서 $Q_c = 3500 BTU/s$, $z = 30 ft$ 일때 계산해보면 $m = 111.45 lb/s$ 가 나온다.
문제에서 주어진 연기 밀도 $ 0.075 lb/ft^3 $으로 나눠보면 $1,486 ft^3 /s = 89,160 ft^3/m$ 이 나와 답이 B이다.
문제에서 10ft 이상으로 연기층을 storage 상부보다 유지시키기 위한 조건이 이 만큼의 연기를 배출하는건데, 만약 10ft 이상이 아니라 더 높이 연기층을 유지하려면 z값이 더 커지므로, $z^{(5/3)}$ 이 부분이 더 커져서 결과적으로 필요한 연기 배출량 m이 더 커지게 될 것이다.
여기까지는 이해했는데, 화재가 난 방의 높이나 넓이에 따라서 연기층의 높이가 달라질텐데 이런건 고려 안해도 되는건가? 이거는 잘 모르겠다. 일단 문제 맞았으니 넘어가지 뭐..
